At ValidExamDumps, we consistently monitor updates to the CompTIA DY0-001 exam questions by CompTIA. Whenever our team identifies changes in the exam questions,exam objectives, exam focus areas or in exam requirements, We immediately update our exam questions for both PDF and online practice exams. This commitment ensures our customers always have access to the most current and accurate questions. By preparing with these actual questions, our customers can successfully pass the CompTIA DataX Certification Exam exam on their first attempt without needing additional materials or study guides.
Other certification materials providers often include outdated or removed questions by CompTIA in their CompTIA DY0-001 exam. These outdated questions lead to customers failing their CompTIA DataX Certification Exam exam. In contrast, we ensure our questions bank includes only precise and up-to-date questions, guaranteeing their presence in your actual exam. Our main priority is your success in the CompTIA DY0-001 exam, not profiting from selling obsolete exam questions in PDF or Online Practice Test.
Given matrix
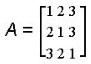
Which of the following is AT?
A)

B)

C)

D)
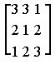
Transposing swaps rows and columns, so the (i, j) entry becomes the (j, i) entry.
A data scientist wants to predict a person's travel destination. The options are:
Which of the following models would best fit this use case?
You need a supervised multiclass classification model to predict one of the four labeled destinations. Linear Discriminant Analysis is designed for such tasks, finding the linear boundaries that best separate the known destination classes.
Which of the following best describes the minimization of the residual term in a ridge linear regression?
Ridge regression extends ordinary least squares by adding an L2 penalty on the coefficients, but it still minimizes the sum of squared residuals (e) as its loss term.
Which of the following explains back propagation?
Back propagation computes the gradient of the loss (error) with respect to each weight by propagating the error signal backward through the network, then uses those gradients to adjust weights and biases.
A data scientist is standardizing a large data set that contains website addresses. A specific string inside some of the web addresses needs to be extracted. Which of the following is the best method for extracting the desired string from the text data?